 |

|
|
|
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
SlayEngine
Captain

Anmeldungsdatum: 10.10.2009
Beiträge: 596
Wohnort: HAJ
 |
 Verfasst am: So Apr 03, 2011 9:48 am Titel: Herleitung der Bernoulli-Gleichung - Verständnisfrage - Verfasst am: So Apr 03, 2011 9:48 am Titel: Herleitung der Bernoulli-Gleichung - Verständnisfrage - |
 |
|
Hallo Leute...
Da in einer Woche meine Physik GFS über den Auftrieb beim Segelflugzeug gehalten werden muss und ich den letzten Teil der Bernoulli-Herleitung nicht vestehe, komme ich mal zu Euch.
Also folgender Teil:

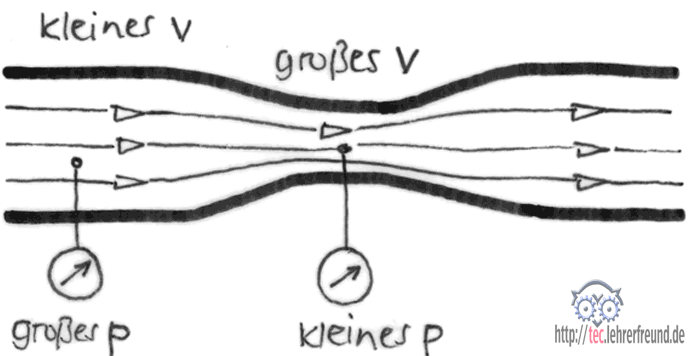
Wie ihr seht wird die Differenz der Arbeit, um das Luftpaket am verengenden Querschnitt eines Rohres zu beschleunigen mit der kinetischen Energie - die ebenso die Arbeit zum Beschleunigen beschreibt - gleichgesetzt.
Das jetzt zum Bisherigen.
Wisst ihr, wie ich von der 2. Gleichung zur 3. komme?
Also: (p a - p b) .... zu pa + 1/2...
Einfaches gleichsetzen??? Irgendwie häng ich da noch.
Vielen Dank schonmal
Zuletzt bearbeitet von SlayEngine am Di Jan 30, 2024 4:36 pm, insgesamt einmal bearbeitet |
|
| Nach oben |
|
 |
|
|
 |
 |
 |
 |
 |
coolmadmat
Captain

Anmeldungsdatum: 02.04.2007
Beiträge: 1311
 |
 Verfasst am: So Apr 03, 2011 10:12 am Titel: Verfasst am: So Apr 03, 2011 10:12 am Titel: |
 |
|
ich gebe mal Hilfe zur Selbsthilfe... :
http://de.wikipedia.org/wiki/Str%C3%B6mung_nach_Bernoulli_und_Venturi
Da steht zumindest wie man darauf kommen kann. Allerdings weià ich nicht wie weit Du mit Mathe in der Schule bist. Eigentlich ist nur dann eine Herleitung sinnvoll wenn man integrieren und mit Skalaren rechnen kann. Ich denke mal, dass es für die Schule ausreicht wenn Du ansprichst wie man es herleiten kann... es sei denn Du hast Mathe und Physik LK und bist im 13ten Schuljahr... 
_________________
âTo oberserve without evaluating is the highest form of human intelligenceâ. - Jiddu Krishnamurti |
|
| Nach oben |
|
 |
|
|
 |
 |
 |
 |
 |
möchtegern_pilot
Captain

Anmeldungsdatum: 08.01.2010
Beiträge: 448
 |
 Verfasst am: So Apr 03, 2011 10:51 am Titel: Verfasst am: So Apr 03, 2011 10:51 am Titel: |
 |
|

Ich glaube da ist ein Vorzeichenfehler dabei in der ersten Zeile.
Da die Summe der Leistungen 0 ergeben muss (adiabates System) gilt:
dW(Druck) + dW(Geschw.) = 0
hier also:
dW(Druck) = - dW(geschw.)
dann den Volumenstrom V kürzen und der Rest sollte dann von alleine Klappen. |
|
| Nach oben |
|
 |
|
|
 |
 |
 |
 |
 |
coolmadmat
Captain

Anmeldungsdatum: 02.04.2007
Beiträge: 1311
 |
 Verfasst am: So Apr 03, 2011 11:40 am Titel: Verfasst am: So Apr 03, 2011 11:40 am Titel: |
 |
|
oh, hatte das wohl falsch verstanden. 
_________________
âTo oberserve without evaluating is the highest form of human intelligenceâ. - Jiddu Krishnamurti |
|
| Nach oben |
|
 |
|
|
 |
 |
 |
 |
 |
SlayEngine
Captain

Anmeldungsdatum: 10.10.2009
Beiträge: 596
Wohnort: HAJ
 |
 Verfasst am: So Apr 03, 2011 8:03 pm Titel: Verfasst am: So Apr 03, 2011 8:03 pm Titel: |
 |
|
Ne, da ist kein Vorzeichenfehler dabei... Die Quelle ist absolut seriös und richtig (ich werde trotzdem das nochmal mitm Lehrer durchchecken) Es wird eine GFS im Fach Physik Klassenstufe 10 sein. Die Herleitung ist bis dahin gut verständlich... Ich finde es lediglich etwas trocken... Ãber Flaps/Slats und Co zu reden ist dann schon interessanter.
Ich hoffe noch auf weitere Antworten, viellt. gibts noch ein Physik-Pro.
Gruà |
|
| Nach oben |
|
 |
|
|
 |
 |
 |
 |
 |
möchtegern_pilot
Captain

Anmeldungsdatum: 08.01.2010
Beiträge: 448
 |
 Verfasst am: So Apr 03, 2011 9:38 pm Titel: Verfasst am: So Apr 03, 2011 9:38 pm Titel: |
 |
|
Doch, da ist ein Vorzeichenfehler drin.
alternativ kannst auch (vb²-va²) statt (va²-vb²) nehmen, ist aber identisch mit dem Vorzeichenfehler.
Gehen wirs mal durch, von 2 nach 3:
V kürzen gibt
pa - pb = rho/2 * (vb² - va²)
Klammer ausmultiplizieren
pa - pb = rho/2 * vb² - rho/2 * va²
auf die richtige Seite
pa + rho/2 * va² = pb + rho/2 * vb²
Weiterer Beweis für VZF:
da pa > pb muss der linke Teil der 2. Gl. >0 sein.
da es eine Gleichung ist muss der rechte Teil ebenfalls >0 sein.
Weil im rechten Teil aber vb² > va² ist (Kontinuität) und damit die rechte Klammer <0 geht die Gleichung in keinem Fall auf.
Aber ich muss jetzt mal weiter auf meine Aerodynamikprüfung nächste Woche lernen... |
|
| Nach oben |
|
 |
|
|
 |
 |
 |
 |
 |
SlayEngine
Captain

Anmeldungsdatum: 10.10.2009
Beiträge: 596
Wohnort: HAJ
 |
 Verfasst am: Mo Apr 04, 2011 11:25 am Titel: Verfasst am: Mo Apr 04, 2011 11:25 am Titel: |
 |
|
| Alles klar, ich habs verstanden... Also, vielen Dank nochmals. |
|
| Nach oben |
|
 |
|
|
 |
 |
 |
 |
 |
|
 |
| |
 |
|
|
Du kannst keine Beiträge in dieses Forum schreiben.
Du kannst auf Beiträge in diesem Forum nicht antworten.
Du kannst deine Beiträge in diesem Forum nicht bearbeiten.
Du kannst deine Beiträge in diesem Forum nicht löschen.
Du kannst an Umfragen in diesem Forum nicht mitmachen.
|
|
|
 |